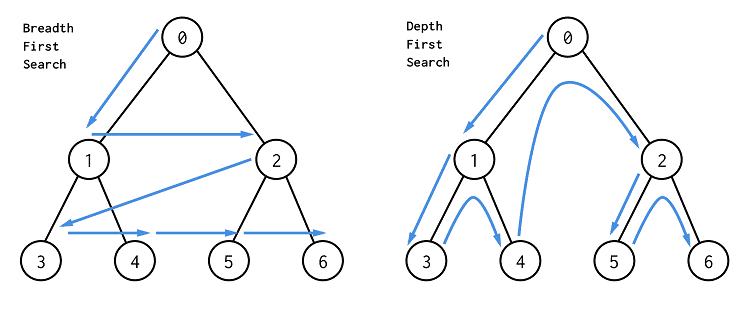
DFS vs BFS
📌 Let’s compare
| BFS | DFS | |
|---|---|---|
| Full form | Breadth-First Search | Depth-First Search |
| Data structure often used | BFS uses Queue data structure to save the nodes which is already visited for finding the shortest path. (FIFO) | DFS uses Stack data structure to save the nodes which is already visited (LIFO) |
| Features | BFS is better when target is closer to Source. -> There is no need of backtracking. | DFS is better when target is far from source -> There is a need of backtracking. -> There is a possibility that it visit all nodes. |
| Advantages | A BFS will find the shortest path between the starting point and any other reachable node | - A DFS on a binary tree generally requires less memory than BFS. - DFS can be easily implemented with recursion. - DFS is faster than BFS. |
| Disadvantages | - A BFS on a binary tree generally requires more memory than a DFS. - BFS is slower than DFS. | A DFS doesn’t necessarily find the shortest path to a node, while DFS does. |
| Situation | - A problem requiring the shortest path | - A problem that you must store the features of each path |
📌 Implementation
1. BFS
- Used queue
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Graph {
private int V;
private LinkedList<Integer> adj[];
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i) adj[i] = new LinkedList();
}
void addEdge(int v, int w) {
adj[v].add(w);
}
/* BFS */
void BFS(int s) {
boolean visited[] = new boolean[V];
LinkedList<Integer> queue = new LinkedList<Integer>();
// Big difference with DFS
// use queue features (FIFO)
visited[s] = true;
queue.add(s);
while (queue.size() != 0) { // = (!queue.isEmpty())
// get the first node and delete it from queue
s = queue.poll();
System.out.print(s + " ");
// get other nodes near the node which visit
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext()) {
int n = i.next();
// if it is not a node which is already visited, check visiting and send to the last
if (!visited[n]) {
visited[n] = true;
queue.add(n);
}
}
/** This expression is also okay
Queue<Integer> q = new LinkedList<Integer>();
q.offer(v);
visited[v] = true;
for (int i = 1; i < n+ 1 ; i++) {
if (map[vv][i] == 1 && !visited[i]) {
q.offer(i); // visit map[vv][i~n]
visited[i] = true;
}
}
**/
}
}
}
2. DFS
- Used stack
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
static int map[][];
static boolean[] visited;
static String answer = "";
public static void dfs_stack(int v) {
Stack<Integer> stack = new Stack<Integer>();
stack.push(v);
while (!stack.isEmpty()) {
int vv = stack.pop();
visited[vv] = true;
answer += vv + " ";
for (int i = 1; i < n + 1; i++) {
if (map[vv][i] == 1 && !visited[i]) {
stack.push(i);
break; // Big difference with BFS
}
}
}
}
- Used recursion
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Graph {
private int V;
private LinkedList<Integer> adj[];
Graph(int v) {
V = v;
adj = new LinkedList[v];
// initialization
for (int i=0; i < v; ++i) adj[i] = new LinkedList();
}
void addEdge(int v, int w) {
adj[v].add(w);
}
/* DFS */
void DFS(int v) {
boolean visited[] = new boolean[V];
// Big difference with BFS
// recursion with v as the starting node
DFSUtil(v, visited);
}
// recursion
void DFSUtil(int v, boolean visited[]) {
// store the node already is visited
visited[v] = true;
System.out.print(v + " ");
// get other nodes near the node which visit
Iterator<Integer> it = adj[v].listIterator();
while (it.hasNext()) {
int n = it.next();
// if it is not a node which is already visited, revoke DFSUtil
if (!visited[n]) DFSUtil(n, visited);
}
}
}
- ** the source
- https://devuna.tistory.com/32

Comments powered by Disqus.